14 LeetCode Patterns to Solve Any Question
The only 14 patterns you'll ever need to master LeetCode Interviews!
If you prefer to watch this in video format with animations, watch it below!
Instead of memorizing hundreds of LeetCode questions and answers, learn generalized patterns to solve any question.
Today, I will teach you all the coding patterns you need to know, when to use them, what the benefit of the pattern is, a visual example, a code template to follow, and LeetCode questions you should solve to master the pattern.
1. Sliding Window
When to use it?
Linear data structures (arrays, lists, strings)
Must scan through a subarray or substring
When the subarray must satisfy some condition (shortest/longest/min/max)
Improve time complexity from O(N^2) to O(N)
Technique
In the sliding window, you have 2 pointers, i and j. Move j as far as you can until your condition is no longer valid, then move the i pointer closer to j until the condition is valid again to shrink the window. At every iteration, keep track of the min/max length of the subarray for the result. Without the sliding window technique, we would need to use a double for loop resulting in O(N^2) time. The sliding window is O(N) time complexity.
Dynamic Sliding Window
In the dynamic sliding window, the size of the window (subarray between i and j) changes throughout the algorithm. In this example, we scan the subarray “bacb” and find that we have a duplicate “b”, so we will move the i pointer to shrink the window and move on to letter “a”, resulting in “acb”, then we start moving j again.
Fixed Sliding Window
In the fixed sliding window, the size of the window is the same length throughout the algorithm. In this case, we need scan subarrays of length 3 for the final result, so we initialize i and j to indices 0 and 2 and at every iteration we increment i and j by 1.
Coding Templates
"""
A generic template for dynamic sliding window finding min window length
"""
def shortest_window(nums, condition):
i = 0
min_length = float('inf')
result = None
for j in range(len(nums)):
# Expand the window
# Add nums[j] to the current window logic
# Shrink window as long as the condition is met
while condition():
# Update the result if the current window is smaller
if j - i + 1 < min_length:
min_length = j - i + 1
# Add business logic to update result
# Shrink the window from the left
# Remove nums[i] from the current window logic
i += 1
return result
"""
A generic template for dynamic sliding window finding max window length
"""
def longest_window(nums, condition):
i = 0
max_length = 0
result = None
for j in range(len(nums)):
# Expand the window
# Add nums[j] to the current window logic
# Shrink the window if the condition is violated
while not condition():
# Shrink the window from the left
# Remove nums[i] from the current window logic
i += 1
# Update the result if the current window is larger
if j - i + 1 > max_length:
max_length = j - i + 1
# Add business logic to update result
return result
"""
A generic template for sliding window of fixed size
"""
def window_fixed_size(nums, k):
i = 0
result = None
for j in range(len(nums)):
# Expand the window
# Add nums[j] to the current window logic
# Ensure window has size of K
if (j - i + 1) < k:
continue
# Update Result
# Remove nums[i] from window
# increment i to maintain fixed window size of length k
i += 1
return resultLeetCode Questions
2. Two Pointers
When to use it?
Linear data structures (arrays, lists, strings)
When you need to scan the start and end of a list
When you have a sorted list and need to find pairs
Removing duplicates or filtering
Technique
Instead of scanning all possible subarrays or substrings, use two pointers i and j at the ends of a string or sorted array to be clever how you increment i or decrement j as you scan the input. This will lower your time complexity from O(N^2) to O(N). In the example above, to detect if a string is a palindrome we scan the ends of the string one character at a time. If the characters are equal, move i and j closer together. If they are not equal, the string is not a palindrome.
Coding Templates
def two_pointer_template(input):
# Initialize pointers
i = 0
j = len(input) - 1
result = None
# Iterate while pointers do not cross
while i < j:
# Process the elements at both pointers
# Adjust the pointers based on specific conditions
# i += 1 or j -= 1
# Break or continue based on a condition if required
# Return the final result or process output
return resultLeetCode Questions
3. Slow and Fast Pointers
When to use it?
Linear data structures (arrays, lists, strings)
Detect cycle in linked list
Find middle of linked list
Perform in one pass with O(1) space
Technique
Use two pointers, a slow and fast pointer. Slow moves once and fast moves twice at every iteration. Instead of using a data structure to store previous nodes to detect a cycle which requires O(N) space, using the two pointer technique will find a cycle with O(1) space if fast loops around the cycle and will eventually meet slow. You can also use this technique to find the middle of a linked list in O(1) space and 1 pass.
Coding Templates
def slow_fast_pointers(head):
# Initialize pointers
slow = head
fast = head
result = None
# move slow once, move fast twice
while fast and fast.next:
slow = slow.next
fast = fast.next.next
# update result based on custom logic
# Example: if fast == slow then cycle is detected
return resultLeetCode Questions
4. In Place Linked List Reversal
When to use it?
Reverse a linked list in 1 pass and O(1) space
Reverse a specific portion of a linked list
Reverse nodes in groups of k
Technique
Use two pointers, prev and ptr which point to the previous and current nodes. To reverse a linked list, ptr.next = prev. Then, move prev to ptr and move ptr to the next node. At the end of the algorithm, prev will point to the head of the reversed list.
Coding Templates
def reverse_linked_list(head):
prev = None
ptr = head
while ptr:
# Save the next node
next_node = ptr.next
# Reverse the current node's pointer
ptr.next = prev
# Move the pointers one step forward
prev = ptr
ptr = next_node
# prev is the new head after the loop ends
return prevLeetCode Questions
5. Binary Search
When to use it?
Input is sorted and you need to find a number
Finding the position of insertion in a sorted list
Handling duplicates in sorted arrays
Searching in rotated sorted arrays
Technique
Start left and right pointers at indices 0 and n-1, then find the mid point and see if that is equal to, less than, or greater than your target. If nums[mid] > target, go left by moving the right pointer to mid-1. If nums[mid] < target, go right by moving left to mid+1. Binary Search reduces search time complexity from O(N) to O(NLogN)
Modified Binary Search
You may be required to find the leftmost or rightmost target value in an array containing duplicates.
You may be required to find a target in a rotated sorted array.
Coding Templates
"""
Classic binary search algorithm that finds a target value
"""
def classic_binary_search(array, target):
left, right = 0, len(array)-1
while left <= right:
mid = left + (right - left) // 2
if array[mid] == target:
return mid
elif array[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
"""
A generic template for binary search such that the returned value
is the minimum index where condition(k) is true
Example 1:
array = [1,2,2,2,3]
target = 2
binary_search(array, lambda mid: array[mid] >= target) --> 1
Example 2:
array = [1,2,2,2,3]
target = 2
binary_search(array, lambda mid: array[mid] > target) --> 4
"""
def binary_search(array, condition):
left, right = 0, len(array)
while left < right:
mid = left + (right - left) // 2
if condition(mid):
right = mid
else:
left = mid + 1
return left
"""
Binary search algorithm that can search a rotated array
by selected the appropriate half to scan at each iteration
"""
def binary_search_rotated_array(array, target):
left, right = 0, len(array)-1
while left <= right:
mid = (left + right) // 2
if array[mid] == target:
return mid
# left side sorted
if array[left] <= array[mid]:
# if target is contained in left sorted side, go left
if array[left] <= target <= array[mid]:
right = mid - 1
else:
left = mid + 1
# right side sorted
else:
# if target is contained in right sorted side, go right
if array[mid] <= target <= array[right]:
left = mid + 1
else:
right = mid - 1
return -1LeetCode Questions
6. Top K Elements
When to use it?
Find the top k smallest or largest elements
Find the kth smallest or largest element
Find the k most frequent elements
Technique
You can always sort an array and then take the first or last k elements, however the time complexity would be O(NLogN). A heap can pop and push elements in O(Log(K)) where K is the size of the heap. Therefore, instead of sorting, we can use a heap to hold the smallest or largest K values, and for every element in the array check whether to pop/push to the heap, resulting in a time complexity of O(NLogK).
Coding Templates
"""
A generic template for the Top K Smallest elements.
"""
import heapq
def top_k_smallest_elements(arr, k):
if k <= 0 or not arr:
return []
# Use a max heap to maintain the k smallest elements
max_heap = []
for num in arr:
# Python does not have a maxHeap, only min Heap
# Therefore, negate the num to simulate a max heap
heapq.heappush(max_heap, -num)
if len(max_heap) > k:
heapq.heappop(max_heap)
# Convert back to positive values and return
return [-x for x in max_heap]
"""
A generic template for the Top K Largest elements.
"""
import heapq
def top_k_largest_elements(arr, k):
if k <= 0 or not arr:
return []
# Use a min heap to maintain the k largest elements
min_heap = []
for num in arr:
heapq.heappush(min_heap, num)
if len(min_heap) > k:
heapq.heappop(min_heap)
return min_heapLeetCode Questions
7. Binary Tree Traversal
When to use it?
Preorder: Serialize or deserialize a tree
Inorder: Retrieve elements in sorted order (BSTs)
Postorder: Process children before parent (bottom-up)
BFS: Level by level scanning
Technique
For the preorder, inorder, and postorder traversals use recursion (DFS). For the level by level scan use BFS iteratively with a queue.
Coding Templates
"""
Preorder traversal: visit node, then left subtree, then right subtree.
"""
def preorder_traversal(node):
if not node:
return
# visit node
preorder_traversal(node.left)
preorder_traversal(node.right)
"""
Inorder traversal: visit left subtree, then node, then right subtree.
"""
def inorder_traversal(node):
if not node:
return
inorder_traversal(node.left)
# visit node
inorder_traversal(node.right)
"""
Postorder traversal: visit left subtree, then right subtree, then node
"""
def postorder_traversal(node):
if not node:
return
postorder_traversal(node.left)
postorder_traversal(node.right)
# visit node
"""
BFS traversal: Visit all nodes level by level using a queue
"""
from collections import deque
def bfs_traversal(root):
queue = deque([root])
while queue:
node = queue.popleft()
if node:
# visit node
queue.append(node.left)
queue.append(node.right)LeetCode Questions
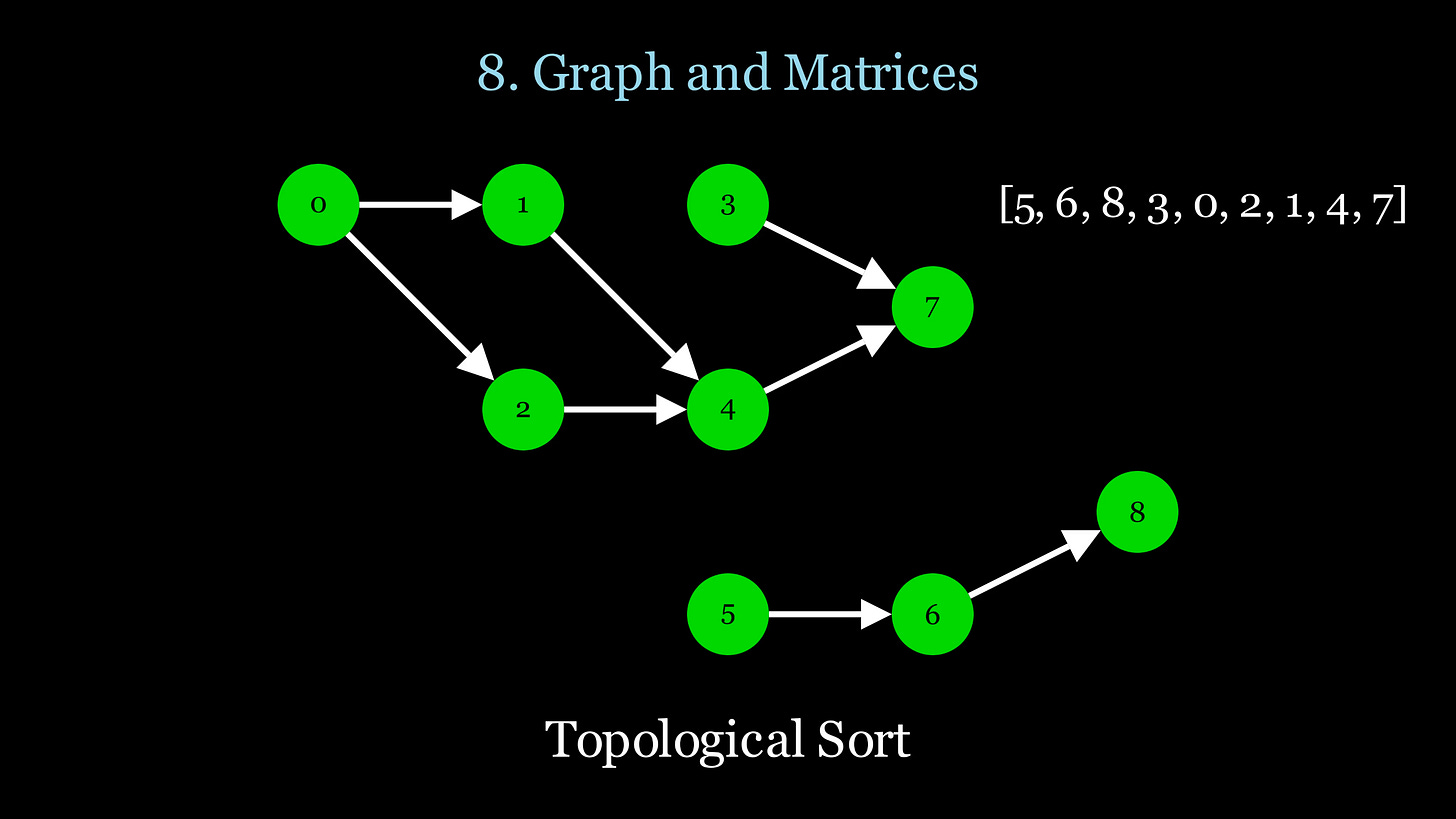
8. Graph and Matrices
When to use it?
Search graphs or matrices
DFS: Explore all possible paths (e.g., maze)
BFS: Find the shortest path
Topological Sort: Order tasks based on dependencies
Technique
DFS (Depth-First Search) traverses as deep as possible along each branch before backtracking, prioritizing visiting nodes or cells in a recursive or stack-based manner. BFS (Breadth-First Search) explores all neighbors of a node or cell before moving deeper, traversing level by level using a queue. For DFS use recursion with a visited set to keep track of visited nodes. For BFS use iteration with a queue and a visited set to keep track of visited nodes. In a graph, neighbors are found in the adjacency list. In a matrix, neighbors are up/down/left/right cells, with some examples including diagonals too.
Coding Templates
"""
DFS for a graph represented as an adjacency list
"""
def dfs(graph):
visited = set()
result = []
def explore(node):
visited.add(node)
result.append(node) # process node
for neighbor in graph[node]:
if node not in visited:
explore(neighbor)
def dfs_driver(graph):
for node in graph:
if node not in visited:
explore(node)
dfs_driver()
return result
"""
BFS for a graph represented as an adjacency list
"""
from collections import deque
def bfs(graph, start):
visited = set()
result = []
queue = deque([start])
while queue:
node = queue.popleft()
if node not in visited:
visited.add(node)
result.append(node) # process node
for neighbor in graph[node]:
queue.append(neighbor)
return result
"""
Topological Sort only works on DAG graphs with no cycles
"""
def topological_sort(graph):
visited = set()
topo_order = []
def hasCycle(node, curpath):
visited.add(node)
curpath.add(node)
for neighbor in graph[node]:
if neighbor in curpath: # cycle detected, no topo sort
return True
if neighbor in visited:
continue
if hasCycle(neighbor, curpath):
return True
curpath.remove(node)
topo_order.append(node) # process node
return False
for node in graph:
if node not in visited:
if hasCycle(node, set()):
return None # cycle detected, no topo sort
# reverse to get the correct topological order
return topo_order[::-1]
"""
DFS for a matrix, visiting all connected cells.
"""
def dfs_matrix(matrix):
m, n = len(matrix), len(matrix[0])
visited = set()
result = []
def explore(i, j):
if not (0 <= i < m and 0 <= j < n):
return
if ((i,j)) in visited:
return
visited.add((i,j))
result.append(matrix[i][j]) # process the cell
# Explore neighbors (up, down, left, right)
for deltaI, deltaJ in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
explore(i + deltaI, j + deltaJ)
def dfs_driver():
for i in range(m):
for j in range(n):
if (i, j) not in visited:
explore(i, j)
dfs_driver()
return result
"""
BFS for a matrix, visiting all connected cells.
"""
from collections import deque
def bfs_matrix(matrix, startI, startJ):
m, n = len(matrix), len(matrix[0])
visited = set()
result = []
queue = deque([(startI,startJ)])
while queue:
i, j = queue.popleft()
if not (0 <= i < m and 0 <= j < n):
continue
if ((i,j)) in visited:
continue
visited.add((i,j))
result.append(matrix[i][j]) # process the cell
# Enqueue neighbors (up, down, left, right)
for deltaI, deltaJ in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
queue.append((i + deltaI, j + deltaJ))
return resultLeetCode Questions
9. Backtracking
When to use it?
Combinatorial problems (combinations, permutations, subsets)
Constraint satisfaction (Sudoku, N-Queens)
Prune paths using constraints to reduce search space
Technique
Backtracking is closely related to DFS, but with a focus on finding solutions while validating their correctness. If a solution doesn't work, you backtrack by returning to the previous recursive state and trying a different option. Additionally, backtracking uses constraints to eliminate branches that cannot lead to a valid solution, making the search more efficient.
Coding Templates
"""
Generic backtracking template.
"""
def backtrack(candidates, curPath):
# Base case: Check if the solution meets the problem's criteria
if is_solution(curPath):
process_solution(curPath)
return
for candidate in candidates:
if is_valid(candidate, curPath):
# Take the current candidate
curPath.append(candidate)
# Recurse to explore further solutions
backtrack(candidates, curPath)
# Undo the choice (backtrack)
curPath.pop()LeetCode Questions
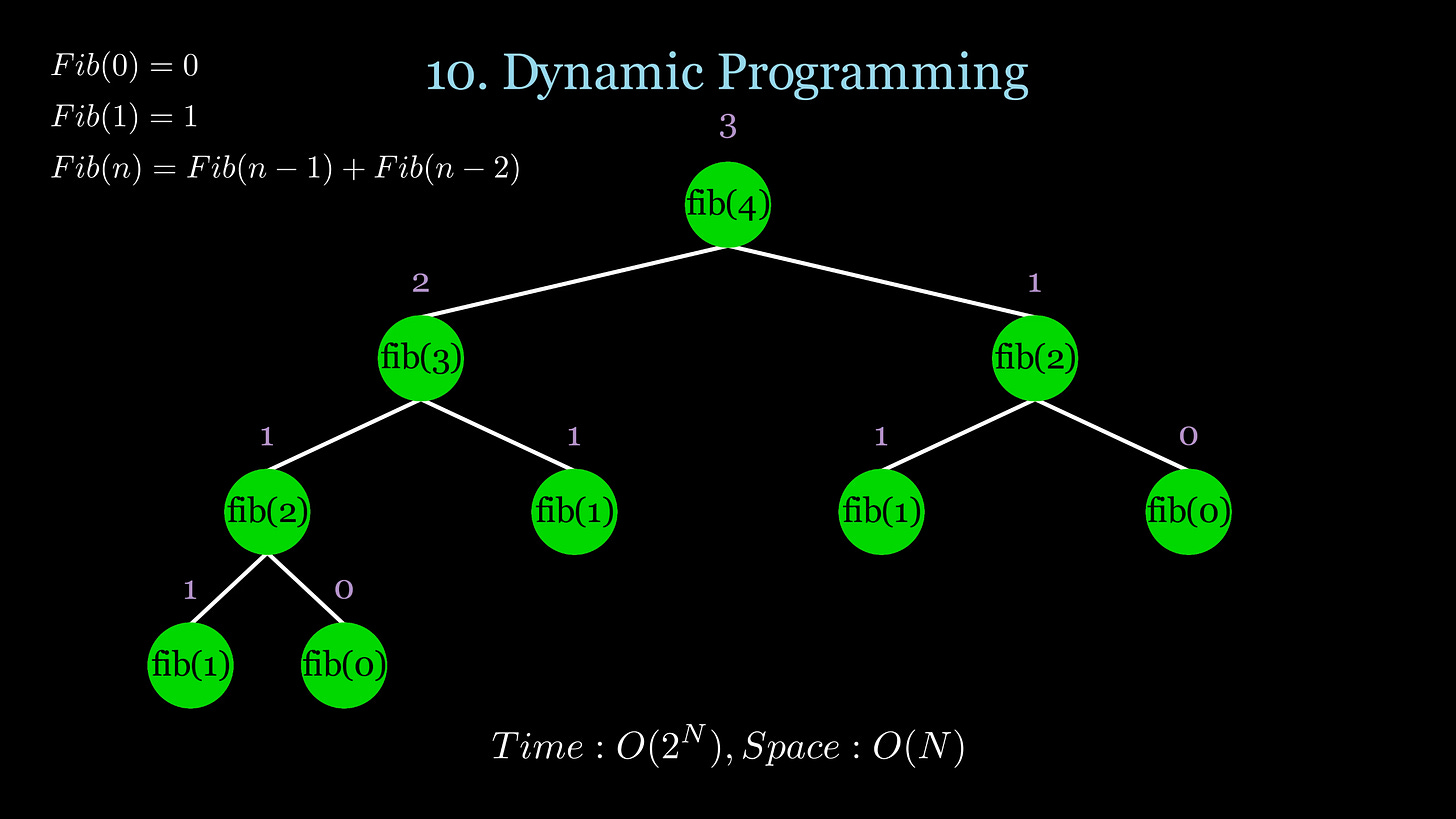
10. Dynamic Programming
When to use it?
Overlapping subproblems and optimal substructure
Optimization problems (min/max distance, profit, etc.)
Sequence problems (longest increasing subsequence)
Combinatorial problems (number of ways to do something)
Reduce time complexity from exponential to polynomial
Technique
Dynamic Programming is used when you need to solve a problem that depends on previous results from subproblems. You can effectively “cache” these previous result values when you calculate them for the first time to be re-used later. Dynamic Programming has 2 main techniques:
Top Down - Recursion (DFS) with Memoization. Memoization is a fancy word for a hashmap that can cache the values previously calculated. In the top down approach you start with the global problem and the recursively split it into subproblems to then solve the global problem.
Bottom Up - Iteratively performed by using an array/matrix to store previous values. In the bottom up approach we start with base cases and then build up to the global solution iteratively.
Many times bottom up is preferred since you can reduce the space complexity if you don’t need access to all subproblems and can store the last couple of subproblem results using variables.
Coding Templates
"""
Top-down recursive Fibonacci without memoization.
Time: O(2^N) | Space: O(N)
"""
def fib_top_down(n):
if n == 0:
return 0
if n == 1:
return 1
return fib_top_down(n-1) + fib_top_down(n-2)
"""
Top-down recursive Fibonacci with memoization.
Time: O(N) | Space: O(N)
"""
def fib_top_down_memo(n, memo={}):
if n in memo:
return memo[n]
if n == 0:
return 0
if n == 1:
return 1
memo[n] = fib_top_down_memo(n-1, memo) + fib_top_down_memo(n-2, memo)
return memo[n]
"""
Bottom-up Fibonacci using an array.
Time: O(N) | Space: O(N)
"""
def fib_bottom_up_array(n):
dp = [0] * (n + 1)
dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
"""
Bottom-up Fibonacci using 2 variables.
Time: O(N) | Space: O(1)
"""
def fib_bottom_up(n):
prev2, prev1 = 0, 1
for i in range(2, n + 1):
fib = prev2 + prev1
prev2 = prev1
prev1 = fib
return prev1LeetCode Questions
11. Bit Manipulation
When to use it?
Count number of 0 or 1 bits in a number
Add numbers without using addition or substraction
Find a missing number in a list
Technique
For bit manipulation, ensure you understand the basic bitwise operators: AND, OR, NOT, XOR and bitwise shifts. Specifically, XOR has interesting properties that allow you to find a missing number in a list or add up 2 numbers without using the addition or subtraction operation. You want to be comfortable with some of the basic bitwise operators, but don’t go too in depth here as these questions can be quite rare.
Coding Templates
"""
Useful bitwise operators for LeetCode
"""
def binary_operators():
return {
"AND": a & b,
"OR": a | b,
"XOR": a ^ b,
"NOT": ~a, # ~a = -a-1 in python
"Left Shift (a << b)": a << b, # left shift 'a' by 'b' bits
"Right Shift (a >> b)": a >> b, # right shift 'a' by 'b' bits
"Mask": a & 1 # gives you the least significant bit of a
}LeetCode Questions
12. Overlapping Intervals
When to use it?
Merge or consolidate ranges
Schedule or find conflicts (e.g. meeting rooms)
Find gaps or missing intervals
Technique
Knowing how to merge overlapping intervals is crucial for these problems.
Usually, you will want to sort the input by the start times so you can guarantee order and always have “a” appear before “b”, making it easier to compare time ranges in chronological order. In the example above, we insert [4,8] into the array, but that eventually gets merged with [3,5], [6,7], and [8,10], into [3,10].
Coding Templates
"""
Generic template for interval problems
"""
def process_intervals(intervals):
# Sort intervals by start time (common preprocessing step)
intervals.sort(key=lambda x: x[0])
# Example: Merged intervals (modify as needed for your problem)
result = []
for interval in intervals:
# If result is empty or no overlap with the last interval in result
if not result or result[-1][1] < interval[0]:
result.append(interval) # Add the interval as is
else:
# Merge overlapping intervals
result[-1][1] = max(result[-1][1], interval[1])
return resultLeetCode Questions
13. Monotonic Stack
When to use it?
Find Next Greater or Smaller Element
Find left/right boundary points in histograms or rectangles
Maintain elements in order to optimize operations
Technique
If you want to find the next greater/smaller element for all elements in an array the brute force approach will take O(N^2). However, with the use of a monotonic stack (either increasing or decreasing order, depending on the problem), we can achieve O(N) time by storing and keeping track of the greatest/smallest elements up until the current iteration. In the example above, notice that we popped 57 from the stack because 69 is greater than 57. However, 76 is greater than 69 so it is a valid solution and we update the output.
Coding Templates
"""
Monotonic increasing stack template.
"""
def monotonic_increasing_stack(arr):
stack = []
for i, num in enumerate(arr):
# Modify condition based on the problem
while stack and stack[-1][0] > num:
stack.pop()
if stack:
pass # process result from top of stack
# Append current value and index
stack.append((num,i))
"""
Monotonic decreasing stack template.
"""
def monotonic_decreasing_stack(arr):
stack = []
for i, num in enumerate(arr):
# Modify condition based on the problem
while stack and stack[-1][0] < num:
stack.pop()
if stack:
pass # process result from top of stack
# Append current value and index
stack.append((num,i))LeetCode Questions
14. Prefix Sum
When to use it?
Cumulative sums are needed from index 0 to any element
Querying subarray sums frequently across multiple ranges
Partial sums can be reused efficiently
Technique
To sum a subarray would take O(N). To sum Q subarrays would take O(N*Q). Can we perform a more efficient algorithm to answer queries? Yes, we can calculate a prefix sum array where
And then we can find the sum of any subarray in O(1) time using the formula
Therefore, we can answer Q queries in O(N) time complexity with a prefix sum.
Coding Templates
"""
Builds the prefix sum array
"""
def build_prefix_sum(arr):
# Initialize prefix sum array
n = len(arr)
prefix = [0] * n
# First element is the same as the original array
prefix[0] = arr[0]
# Build the prefix sum array
for i in range(1, n):
prefix[i] = prefix[i - 1] + arr[i]
return prefix
"""
Queries the sum of elements in a subarray [left, right] using prefix sum.
"""
def query_subarray_sum(prefix, i, j):
if i == 0:
return prefix[j]
return prefix[j] - prefix[i - 1]





























++ Good Post, Also, start here how to build tech, Crash Courses, 100+ Most Asked ML System Design Case Studies and LLM System Design
How to Build Tech
https://open.substack.com/pub/howtobuildtech/p/how-to-build-tech-10-how-to-actually?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/howtobuildtech/p/how-to-build-tech-06-how-to-actually?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/howtobuildtech/p/how-to-build-tech-05-how-to-actually?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/howtobuildtech/p/how-to-build-tech-04-how-to-actually?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/howtobuildtech/p/how-to-build-tech-03-how-to-actually?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/howtobuildtech/p/how-to-build-tech-01-the-heart-of?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/howtobuildtech/p/how-to-build-tech-02-how-to-actually?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
Crash Courses
https://open.substack.com/pub/crashcourses/p/crash-course-09-part-1-hands-on-crash?utm_campaign=post-expanded-share&utm_medium=web
https://open.substack.com/pub/crashcourses/p/crash-course-07-hands-on-crash-course?utm_campaign=post-expanded-share&utm_medium=web
https://open.substack.com/pub/crashcourses/p/crash-course-06-part-2-hands-on-crash?utm_campaign=post-expanded-share&utm_medium=web
https://open.substack.com/pub/crashcourses/p/crash-course-04-hands-on-crash-course?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/crashcourses/p/crash-course-03-hands-on-crash-course?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/crashcourses/p/crash-course-02-a-complete-crash?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/crashcourses/p/crash-course-01-a-complete-crash?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
LLM System Design
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-577?utm_campaign=post-expanded-share&utm_medium=web
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-4ea?utm_campaign=post-expanded-share&utm_medium=web
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-499?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-63c?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-bdd?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-661?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-83b?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-799?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-612?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-7e6?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-67d?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/naina0405/p/most-important-llm-system-design-b31?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://naina0405.substack.com/p/launching-llm-system-design-large?r=14q3sp
https://naina0405.substack.com/p/launching-llm-system-design-2-large?r=14q3sp
[https://open.substack.com/pub/naina0405/p/llm-system-design-3-large-language?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/naina0405/p/important-llm-system-design-4-heart?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
https://open.substack.com/pub/naina0405/p/very-important-llm-system-design-63c?r=14q3sp&utm_campaign=post&utm_medium=web&showWelcomeOnShare=false
I liked the order in which you have given the problems to practice. I just want to tell you about a small correction needed. It's the time complexity of binary search which is mentioned O(NlogN).